Загатки плус (5/5)
|
Логички загатки наменети за пошироката публика. Бројот на жолти ѕвездички ја одредува тежината на загатката.
Расположени сте за уште загатки?
Посетете ја блог категоријата Загатки и хумор. *) Рубриката ја уредува: Ирена Стојковска
|
<
>
Многу одамна си живеело едно племе за кое нилскиот коњ било свето животно. Поглаварот на племето си чувал за милениче нилски коњ кој си го носел секаде со себе и си го хранел. Еднаш годишно, поглаварот го качувал на брод нилскиот коњ и се упатувал кон горниот дел од течението на реката каде се собирале сите жители на племето и каде тој го собирал од нив годишниот данок во злато. За таа цел племето имало една огромна балансирана вага, на која, на едниот тас, поглаварот го ставал нилскиот коњ, а на другиот тас, членовите на племето го ставале златото сѐ додека вагата не била доведена до рамнотежа. Една година, нилскиот коњ пораснал толку многу што кога го ставиле на тасот од вагата, вагата се скршила. Тогаш, поглаварот се налутил и разлутено му се изнавикал на својот Министер за данок: „Го сакам мојот данок во злато додека да зајде сонцето! Ако не го добијам, ќе ти ја отсечам главата!“ Министерот мислел, мислел и до крајот на денот нашол решение. Може ли да кажете кое било решението на Министерот?
Објавена на Facebook: 25 август 2021, 11:35pm Бродот во кој го превозувале нилскиот коњ ќе го искористат за вага. Ќе го сместат нилскиот коњ во бродот и ќе забележат до каде на бродот стигнало нивото на водата. Потоа, кога ќе го извадат нилскиот коњ од бродот, во бродот ќе стваат злато сѐ додека нивото на водата не дојде до обележаното место. На тој начин ќе измерат злато со еднаква маса како и масата на нилскиот коњ.
<
>
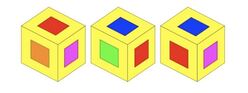
На сликата се прикажани три позиции на една иста коцка која има квадрати во боја на секоја од нејзините страни. Која боја е спротивно од сината боја?
Објавена на Facebook: 31 мај 2021, 07:05аm На спротивната страна на сината боја се наоѓа портокаловата боја.
<
>
Сегашните години на Андреа се разлика од трикратните нејзини години после три години и трикратните нејзини години пред три години. Колку години има Андреа?
Објавена на Facebook: 28 мај 2021, 07:05pm Нека x се сегашните години на Андреа. Тогаш, иамаме x = 3 · (x + 3) - 3 · (x - 3) x = (3x + 9) - (3x - 9) x = 3x + 9 - 3x + 9 x = 18 Значи, Андреа има 18 години.
<
>
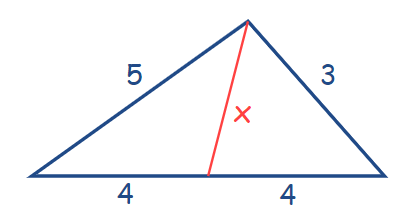
Бидејќи 4 + 4 = 5 + 3, ова значи дека станува збор за дегенерирам триаголник, односно темето меѓу страните со должина 5 и 3 лежи на страната со должина 8. Отсечката до должина x всушност го поврзува тоа теме со средината на страната со должина 8, а знаеме дека тоа теме е одалечено за 5 од едната крајна точка и за 3 од другата крајна точка на основата, значи x = 4 - 3 = 1.
<
>
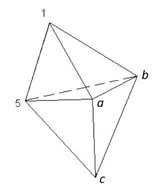
Производот на првите три броја, производот на последните три броја и производот на трите броја во средина е 120 секој (види слика). Кој број треба да биде напишан на средната коцка?
Објавена на Facebook: 24 јануари 2020, 11:09pm Производит на првите три броја е 120, а првиот број е 5, значи производот на вториот и третиот број е 120 : 5 = 24. Проезводот на последните три броја е 120, а последниот број е 6, значи проеизводот на третиот и четвртиот број е 120 : 6 = 20. Ако ги помножиме последниве два проеизвода добиваме 24 · 20 = 480, што претставува проеизвод на вториот, третиот, четвртиот и повторно третиот. Значи, третиот (средниот) број е 480 : 120= 4.
<
>
Братот тргнал 5 минути по сестрата. Ако братот се движи 1,5 пати побрзо од сестрата, за колку време тој ќе ја стигне сестрата?
Објавена на Facebook: 22 јануари 2020, 11:25am Нека почетното растојание, во моментот кога братот тргнал по сестрата е x. За следните 5 минути, сестрата ќе помине уште едно растојание x, додека братот ќе помине 1,5 · x, па растојанието меѓу сестрата и братот ќе се намали од x на 0,5 · x. Па, на братот ќе му требаат уште 5 минути да ја стигне сестрата. Значи, братот ќе ја стигне сестрата за 10 минути.
<
>
Најди број кој завршува на 17, делив е со 17 и збирот на неговите цифри му е еднаков на 17.
Објавена на Facebook: 20 јануари 2020, 11:57am Бројот x завршува на 17, па може да го запишеме како y17 (во позициона форма). Toj е делив со 17, тогаш и бројот x - 17 = y00 е исто така делив со 17. Од друга страна y00 завршува на две нули, па е делив со 100, а 17 и 100 се заемно прости, односно немаат заеднички делител поголем од 1, па и y е делив со 17. Збирот на цифри на x е 17, па збирот на цифри на y е 17 - (1 + 7) = 17 - 8 = 9. Задачата ја сведовме на барање на број y кој има збир на цифри 9 и е делив со 17. Бројот y е делив и со 9 (затоа што збирот на цифри му е 9), 9 и 17 се заемно прости, па следи дека y е делив со 9 · 17 = 153. Првиот таков број е y = 153. Значи, x = 15317. Да забележиме дека постојат и други броеви кои ги исполнуваат зададените услови.
<
>
Објавена на Facebook: 13 јуни 2019, 1:13pm Бидејќи 1 + 5 + а = 1+ c + a, следи c = 5. Потоа, од 1 + 5 + а = а + 5 + b, следи дека a = b. Од 1 + 5 + а = 1 + b + a, следи дека b=5, значи и a = 5. Бараните броеви се 5, 5, 1. |
|
Copyright © 2015 Математика +
|